SOURCE- study.com
In the intricate world of financial markets, the Black-Scholes Model stands as a landmark innovation that revolutionized the understanding and pricing of financial derivatives, particularly stock options. Developed by economists Fischer Black, Myron Scholes, and Robert Merton in the early 1970s, this mathematical model has become a cornerstone in option pricing theory. This article delves into the Black-Scholes Model, exploring its fundamental principles, applications, and impact on financial markets.
Understanding the Basics:
The Birth of the Black-Scholes Model:
The Black-Scholes Model emerged during a period of intense financial innovation when options trading was gaining traction. Fischer Black and Myron Scholes, with the later contribution of Robert Merton, sought to develop a mathematical framework that could effectively price European-style options.
The Black-Scholes Equation:
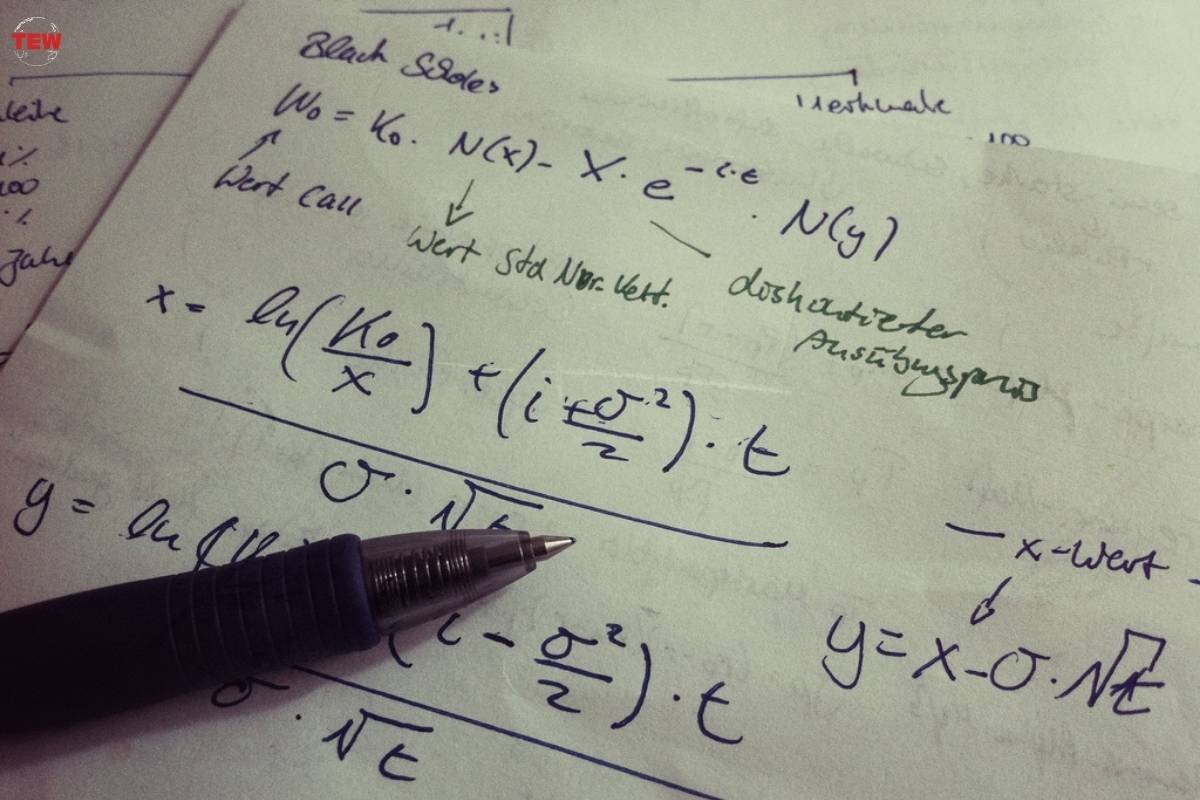
At the heart of the model is the Black-Scholes differential equation, a partial differential equation that describes the price movement of financial instruments over time. This equation provides a theoretical foundation for pricing options based on certain assumptions, including constant volatility and a risk-free interest rate.
Assumptions of the Model:
The Black-Scholes Model operates under several key assumptions:
- Stock prices follow a geometric Brownian motion.
- Volatility remains constant over the option’s life.
- No dividends are paid during the option’s life.
- The risk-free interest rate is constant and known.
- There are no transaction costs or taxes.
The Black-Scholes Formula:
The Black-Scholes Model produced a groundbreaking formula for calculating the theoretical price of a European-style call or put option. The formula is calculated using specific formulas involving the stock price, strike price, time to expiration, volatility, and risk-free rate.
Applications of the Black-Scholes Model:
1. Option Pricing:
The primary application of the Black-Scholes Model is in determining the fair market value of European-style call-and-put options. By inputting the relevant variables into the formula, investors and financial institutions can calculate the theoretical price of an option.
2. Risk Management:

The model facilitates risk management by providing a quantitative framework for assessing and managing the risk associated with options positions. Traders can use the Black-Scholes Model to make informed decisions regarding hedging and portfolio optimization.
3. Market Volatility Assessment:
The model’s incorporation of volatility as a key parameter allows market participants to assess and compare the implied volatility of options with historical volatility. This aids in anticipating potential market movements and adjusting trading strategies accordingly.
4. Financial Decision-Making:
Beyond options trading, the Black-Scholes Model has influenced broader financial decision-making. It serves as a reference point for corporate finance decisions, influencing capital budgeting, investment appraisal, and strategic financial planning.
Critiques and Limitations:
1. Assumption Sensitivity:
The model’s accuracy is highly dependent on the assumptions it makes, such as constant volatility and interest rates. In real-world scenarios, these factors may fluctuate, impacting the reliability of Black-Scholes pricing.
2. European-Style Options Only:
The model is designed specifically for European-style options, which can only be exercised at expiration. American-style options, which allow early exercise, may not be accurately priced using the Black-Scholes Model.
3. Market Dynamics Oversimplification:

The model assumes that stock prices follow a geometric Brownian motion, which may oversimplify the complex dynamics of financial markets. Real-world factors such as market jumps and discontinuities are not fully captured.
4. Neglects Dividends:
The Black-Scholes Model does not account for dividend payments, which is a significant limitation, especially when pricing options on stocks that pay dividends.
Limited Applicability during Financial Crises:
The model’s reliance on constant volatility and risk-free interest rates may lead to inaccurate pricing during periods of financial turbulence when these variables are subject to rapid changes.
Conclusion:
The Black-Scholes Model, despite its limitations, remains a foundational tool in the world of finance. Its impact extends far beyond the realm of options pricing, influencing risk management, financial decision-making, and market dynamics. Over the years, variations and enhancements to the model have been introduced to address its shortcomings and adapt to evolving market conditions.
As financial markets continue to evolve, the Black-Scholes Model serves as a testament to the power of mathematical models in understanding and navigating the complexities of option pricing. While it may not be a one-size-fits-all solution, its contributions have undeniably shaped the landscape of quantitative finance and left an enduring mark on the understanding of derivatives pricing.






